之前做广告预测的竞赛时,从kaggle博客上发现一个可以计算线上测试集正例比例的技巧,将博客的实验和公式推一遍后重新记录下来。 只可惜实际工程中并没有什么用,倒是在比赛中是个不错的技巧。
适用背景
- 预测问题:二分类
-
损失函数:Logloss
原理说明
固定预测值为p,设线上测试集标签的正例比为r,线上测试的损失函数结果为loss,则:
因此固定预测值p,已知线上损失结果loss,可以计算出线上测试集的正例比,且与预测值p无关
观察式2,不难看出:
- 当预测值固定时,logloss与测试集正例比成线性关系
- 已知测试集正例比,当预测值与测试集正例比相等时,logloss最小(即采取随机预测时的logloss结果)
实验结果
# 固定预测值,测试集不同正例比计算得到的logloss如下
predicty = [0.037] * 1000
rLossDf = pd.DataFrame(index=list(range(0,1000)))
rLossDf['loss'] = rLossDf.index.map(lambda x: log_loss([1]*x+[0]*(1000-x), predicty))
rLossDf.index = rLossDf.index / 1000
rLossDf['loss'].plot(figsize=(10,6))
plt.xlabel('测试集中的正例比', fontsize=13)
plt.ylabel('测试集的损失函数值', fontsize=13)
plt.title('固定预测值为0.37时logloss随正例比变化曲线', fontsize=15)
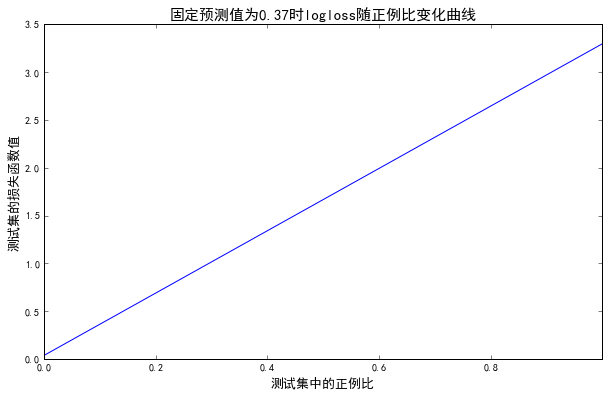
若线上测试得到的logloss为0.61,则可计算出线上测试集的实际正例率为0.278
# 当测试集正例比固定,不同预测值计算得到的logloss如下
ratio = 0.37
testy = [1]*int(1000*ratio)+[0]*int(1000-1000*ratio)
prLossDf = pd.DataFrame(index=list(range(0,1000)))
prLossDf.index = prLossDf.index / 1000
prLossDf['loss'] = prLossDf.index.map(lambda x: log_loss(testy, [x]*1000))
prLossDf['loss'].plot(figsize=(10,6))
plt.xlabel('预测值', fontsize=13)
plt.ylabel('测试集的损失函数值', fontsize=13)
plt.title('当测试集正例比为0.37时,logloss随预测值变化曲线', fontsize=15)
plt.ylim((0.5,2))
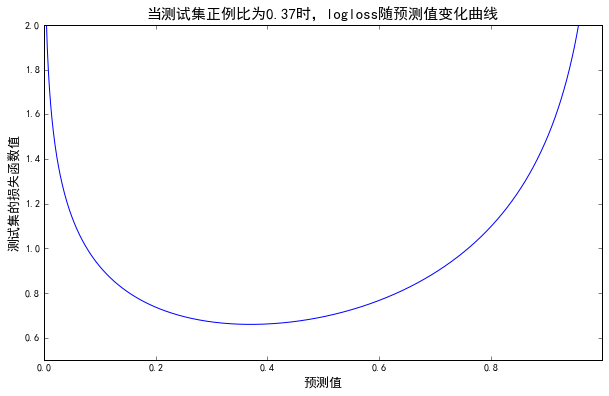
可知当predict=0.37时,得到随机预测的logloss结果为0.659。
参考文献
How many 1’s are in the Public LB? (https://www.kaggle.com/davidthaler/how-many-1-s-are-in-the-public-lb)